Morphological Operations in Image Processing
Image processing is an interesting topic in Computer Science. We have seen some of its basics earlier. This is going to deal with some sensitive important aspects in this big sector. You need to carefully look into the definitions and explanations.
Binary images (consists of pixels that can have one of exactly two colors, usually black and white) may contain numerous imperfections. In particular, noises and textures can be distorted when the binary regions are produced by a simple threshold. Morphological Operations in Image Processing pursue the goal of removing these imperfections by accounting for the form and structure of the image.
A collection of non-linear operations related to the shape or morphology of features in an image is known as Morphological Operation in Image Processing. Morphological operations rely only on the relative ordering of pixel values, not on their numerical values, and therefore are especially suited to the processing of binary images. These techniques can also be extended to greyscale images such that their light transfer functions are unknown and therefore their absolute pixel values are of no or minor interest.
A small shape or template called a structuring element, a matrix that identifies the pixel in the image being processed and defines the neighborhood used in the processing of each pixel is used to probe an image in these Morphological techniques. It is positioned at all possible locations in the input image and compared with the corresponding neighborhood of pixels.
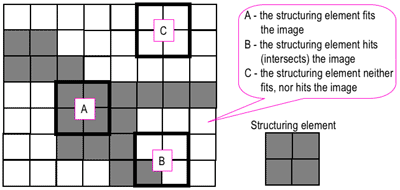
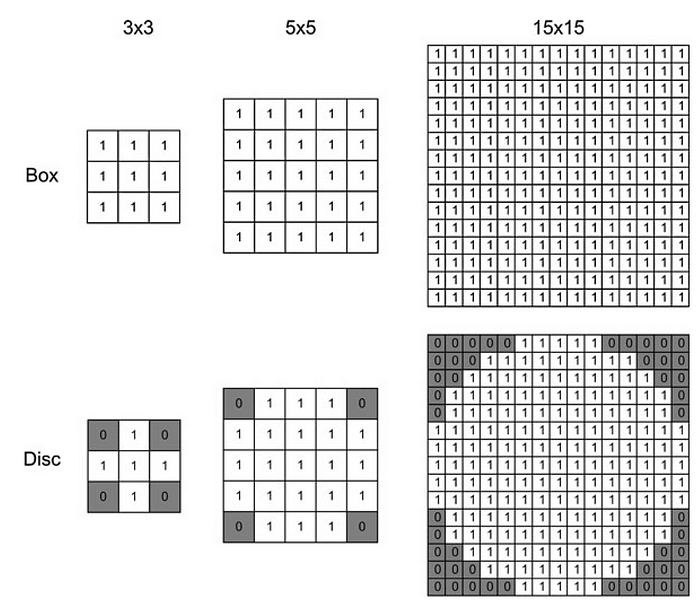
Commonly these structuring elements have odd dimensions and the origin is defined as the center of the matrix. These are playing in morphological image processing the same role as convolution kernels in linear image filtering.
Fundamental operations
- Dilation (represented by the symbol ⊕)
The assigned structuring element is used for probing and expanding the shapes contained in the input image. In Specific, it acts as a local maximum filter. Dilation has the opposite effect on erosion. It adds a layer of pixels to both the inner and outer boundaries of regions.
That is, the value of the output pixel is the maximum value of all pixels in the neighborhood. In a binary image, a pixel is set to 1 if any of the neighboring pixels have the value 1. Morphological dilation makes objects more visible and fills in small holes in objects.

2. Erosion (represented by the symbol ⊖)
Straight opposite to the dilation. The assigned structuring element is used for probing and reducing the shapes contained in the input image. In Specific, it acts as a local minimum filter.
Also, the structuring elements shrink an image by stripping away a layer of pixels from both the inner and outer boundaries of regions. By using erosion, we can eliminate the holes and gaps between different regions to become larger and small details.
That is, The value of the output pixel is the minimum value of all pixels in the neighborhood. In a binary image, a pixel is set to 0 if any of the neighboring pixels have the value 0. Morphological erosion removes islands and small objects so that only substantive objects remain.

Check this clear example

Applications of morphological dilation and erosion operations
- Surface scanning
- Real mechanical surface reconstruction
- Freeform surface deviation evaluation
Compound operations
Morphological operations are represented as combinations of erosion, dilation, and simple set-theoretic operations such as the complement of a binary image, intersection, and union of two or more binary images.

- Opening (A o B=(A⊖B)⊕B)
It is achieved by first eroding an image and then diluting it. Opening removes any narrow connections and lines between two regions.
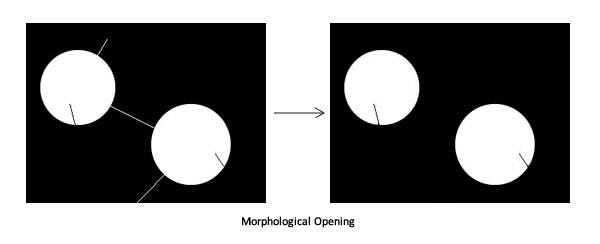
The opening operation erodes an image and then dilates the eroded image, using the same structuring element for both operations. The morphological opening is useful for removing small objects from an image while preserving the shape and size of larger objects in the image.
2. Closing (A • B=(A⊕B)⊖B)
It is done by first dilating the image and then eroding it. The order is the reverse of the opening. Closing fills up any narrow black regions or holes in the image.
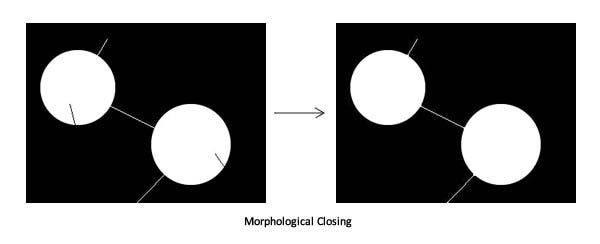
The closing operation dilates an image and then erodes the dilated image, using the same structuring element for both operations. Morphological closing is useful for filling small holes in an image while preserving the shape and size of the objects in the image.
3. Gradient
The difference between the dilation and the erosion of the image. This is used to find boundaries or edges in an image. It is recommended to apply some filtering before calculating the gradient because it is very sensitive to noise.

4. Black hat or Bottom hat
The difference between the closing of an image and the input image itself. This highlights the narrow black regions in the image.

The bottom hat transform closes an image, then subtracts the original image from the closed image. The bottom hat transform can be used to find intensity troughs in a grayscale image.
5. Top hat
The difference between the source or input image and the opening of the source or input image. It highlights the narrow pathways between different regions.

The top hat transform opens an image, then subtracts the opened image from the original image. The top hat transform can be used to enhance contrast in a grayscale image with non-uniform illumination. The transform can also isolate small bright objects in an image.
Applications of morphological Compound operations (Opening and closing)
- Form approximation of functional surfaces for conformable interfaces
- Identifying contact points between two surfaces is non-conforming
- Uncertainty zone for continuous surface reconstruction
- Coin counting and valuation
I hope that you’ve clearly understood and I expect you to try some questions first by hand without using MATLAB or any Image Processing tools to ensure that you have understood the real concept.
To sharpen your knowledge, read Image Processing in Python: Algorithms, Tools, and Methods You Should Know.
Good Luck and enjoy processing the Images.
